All’inizio del nono secolo Alcuino da York, che fu il precettore di Carlo Magno, scrisse le “Propositiones ad Acuendos Juvenes” un opera in latino contenente 53 problemi di carattere ludico. Alcuni di questi riguardano manovre di barche per traghettare persone attraverso un fiume rispettando alcune condizioni. Il più semplice proposto, è diventato celeberrimo, tanto da costituire un detto ancora in uso oggi; “Salvare capra e Cavoli”, è la proposizione numero XVIII:

PROPOSITIO DE HOMINE ET CAPRA ET LUPO.

Homo quidam debebat ultra fluvium transferre lupum, capram, et fasciculum cauli. Et non potuit aliam navem invenire, nisi quae duos tantum ex ipsis ferre valebat. Praeceptum itaque ei fuerat, ut omnia haec ultra illaesa omnino transferret. Dicat, qui potest, quomodo eis illaesis transire potuit?

Un uomo deve attraversare un fiume portando con se un lupo, una capra ed un cavolo, ma la barca è talmente piccola che può trasportare solo un carico per volta, ma non potrà lasciare il lupo solo con la capra, né la capra sola con il cavolo, per ovvi motivi. Come procederà ?

Il problema si diffonde rapidamente e lo ritroviamo riprodotto in molti lavori antichi, e viene riproposto in molti libri di giochi logici ancora oggi. E’ interessante notare che nel “De Viribus Quantitatis” il problema è indicato nell’indice al capitolo LXV , ma poi viene dimenticato nel testo:

Esistono anche versioni fisiche, in Francia durante la Belle Epoque furono prodotte migliaia di scatoline in cartoncino contenenti giochi e rompicapo di vario genere. Uso le figurine di una di queste, “La Chèvre et le Chou” prodotta da JLR (sigla per Le Jeux Reunis. di M.Revanaz e L.Tabernat) per la soluzione:

Sempre in Alcuino, al problema XVII troviamo quello che diverrà noto come “I tre mariti gelosi” proposti qui come 3 fratelli:

XVII. PROPOSITIO DE TRIBUS FRATRIBUS SINGULAS HABENTIBUS SORORES.

Tres fratres erant, qui singulas sorores habebant, et fluvium transire debebant. (Erat enim unicuique illorum concupiscientia in sorore proximi sui) qui venientes ad fluvium non invenerunt, nisi parvam naviculam, in qua non potuerunt amplius nisi duo ex illis transire. Dicat, qui potest, qualiter fluvium transierunt, ne una quidem earum ex ipsis maculata sit?

C’erano tre fratelli che avevano ciascuno una sorella e dovevano attraversare un fiume. Ciascuno di essi desiderava la sorella degli altri. Arrivati a un fiume non trovarono altro che una piccola barca che poteva trasportare solo due di essi. Dica chi può in che modo attraversarono il fiume, in modo che nessuna di esse fosse oltraggiata.

Anche questo lo troviamo in molti lavori medievali, vediamo qui come viene discusso da Tartaglia suo General Trattato dé numeri et misure del 1556:

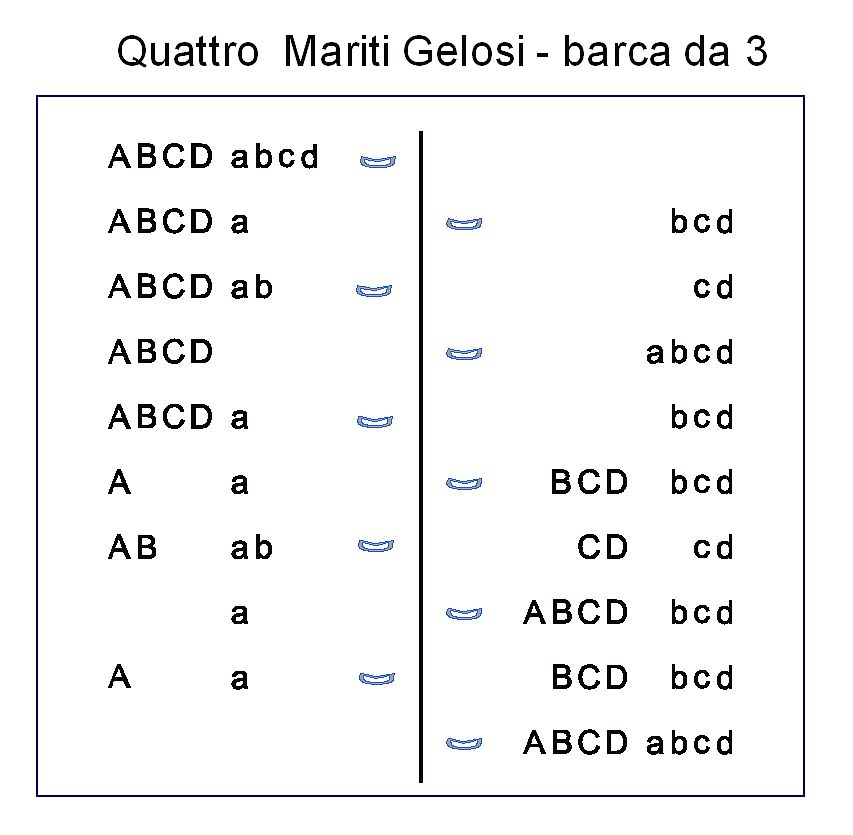
Lo stesso Tartaglia passa poi a dare una propria soluzione nel caso delle 4 coppie , ma qui commette un errore, difatti così come è posto il problema non ammette soluzione.

L’errore fu rilevato da Claude-Gaspar Bachet di Mézirac nel suo ” Problèmes Plaisants & Délectables” 1612 e l’impossibilità fu dimostrata da Edouard Lucas: L’Arithmetique Amusante” 1895. Questo stesso problema può essere risolto o ammettendo l’esistenza un’isola fra le due sponde (M. Cadet de Fontanay 1879), oppure utilizzando una barca che può trasportare 3 persone (M. Labosne). Ecco le due soluzioni:

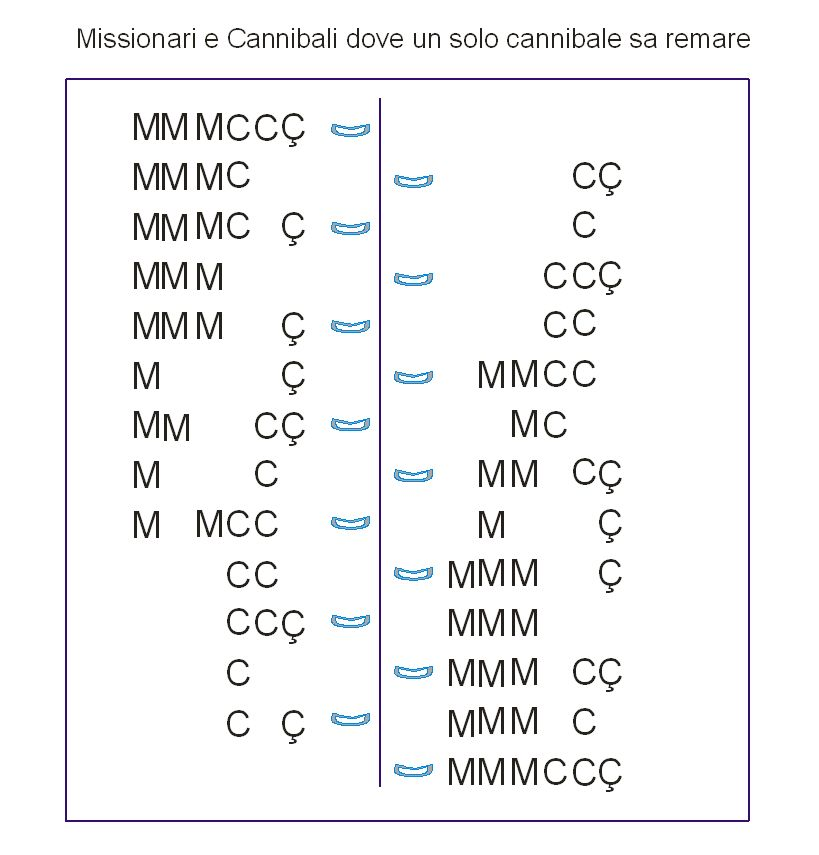
Un’altro problema di attraversamento del fiume , è quello conosciuto come Missionari e Cannibali:

Tre cannibali e tre missionari devono attraversare insieme un fiume da una sponda all’altra, ma per farlo dispongono di una sola barca a due posti, e se a riva si troveranno più cannibali che missionari, per questi sarà la fine.  Sol:

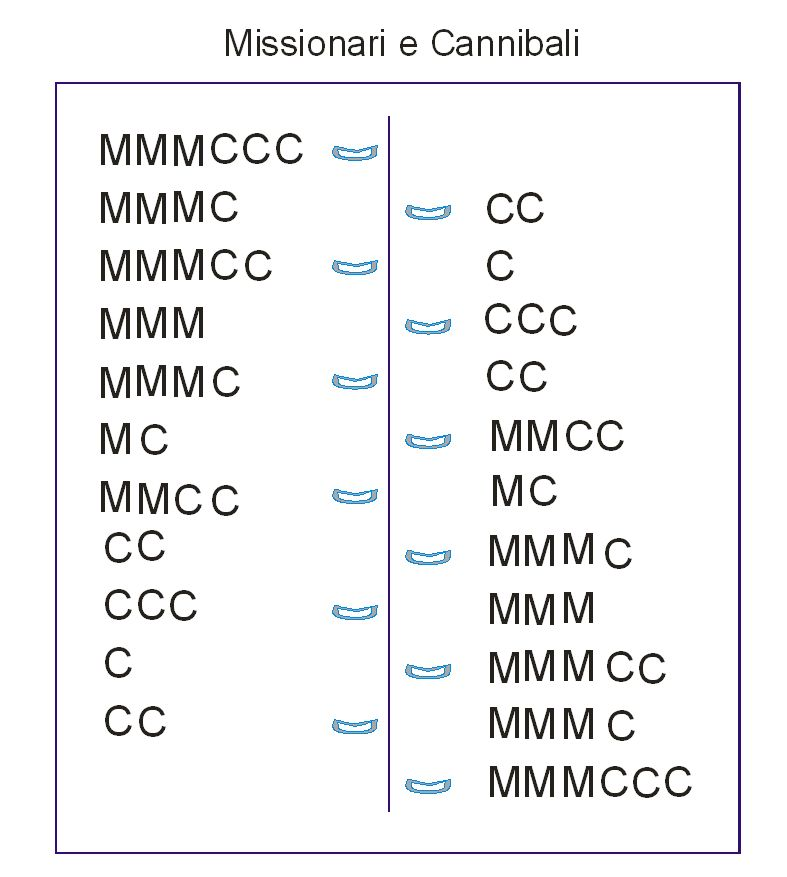
In un’altra versione un solo cannibale è capace di remare: